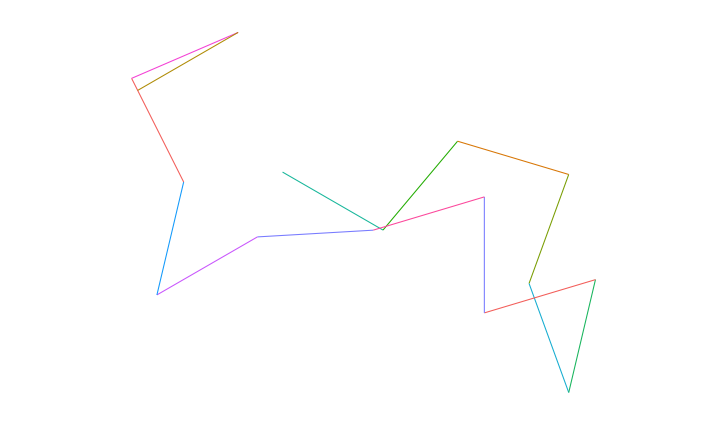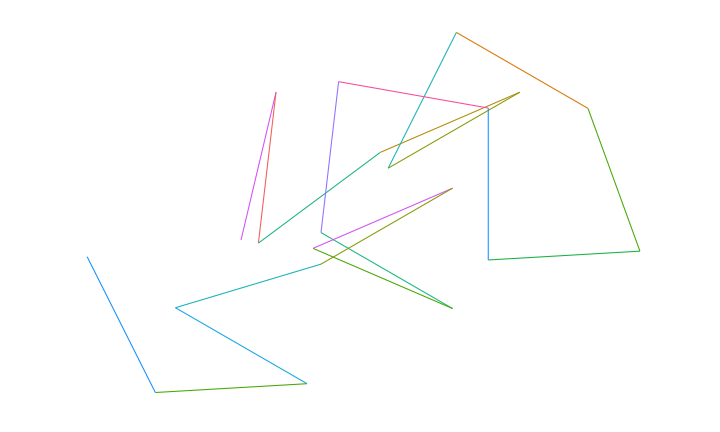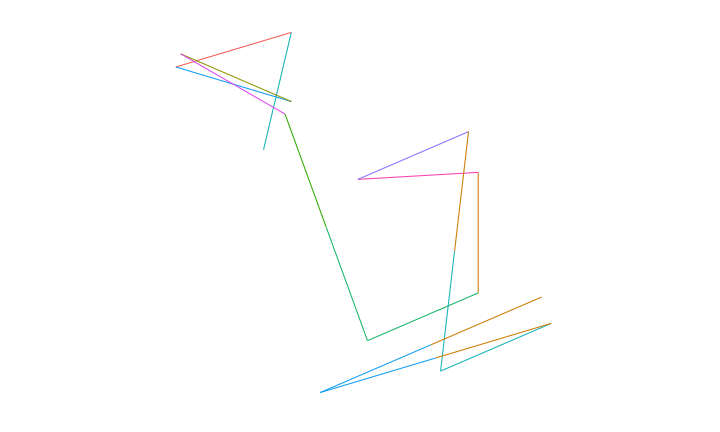Shape of Words
Intro:
After seeing The Art of Pi by Nadieh Bremer I was inspired to use her random-walk style technique to interrogate the shape of other things. Pretty much every irrational number has already been visualized so I figured why not move out of the math domain and into something more… personal.
Many efforts have been made to look into the “shape” of stories (see this post for my take on it,) but not much attention has been paid to a smaller scale. By converting a word or small sentence to a series of numbers and then generating a walk based upon those numbers we are able to construct a kind of fingerprint for any given set of characters. Keep in mind this fingerprint means absolutely nothing and is arbitrary in the most pure sense of the word, but it is interesting none-the-less.
The plotting and walk code is almost unabashedly wholesale taken from Nadieh Bremer’s github repo for her project. If you haven’t checked out her site/work I highly recommend it!
Converting a string to numbers:
We will take a string and split it on each letter. From here we will assign a number from 1-26 to each letter corresponding to their position in the alphabet. E.g. a = 1, b = 2, etc. We allow a space to equal 27.
stringToVec = function(string){
string = tolower(string) #get all the string to lowercase
dict = c(letters, c(" "))
as.vector(sapply(strsplit(string, "")[[1]], function(d){
if(d %in% dict){
return(which(dict == d) ) #ignore non-coded characters
} else return(0)
}))
}
# A simple test:
(test = stringToVec("Hello, World"))## [1] 8 5 12 12 15 0 27 23 15 18 12 4Awesome, now that we have that we just need a way to translate these numbers into a random-walk style coordinate list. We need to scale the domain of to the range so that we can multiply by and get a radian corresponding to some angle around a circle.
toRW = function(vec){
#original code from above linked Bremer github repo.
N <- length(vec)
l <- 27 #the biggest value we can see.
x <- y <- rep(NULL, length(vec))
x[1] <- 0
y[1] <- 0
#Calculate new position for each value, based on the position of the old digit and the
#angle is determined by the digit itself
for (i in 2:length(vec)){
x[i] <- x[(i-1)] + sin((pi*2)*(vec[i]/l)) #scale by largest observed val
y[i] <- y[(i-1)] + cos((pi*2)*(vec[i]/l))
}
#Return the dataframe.
data.frame(val=vec, x=x, y=y, stringsAsFactors=F)
}
#again test this to make sure it's working.
kable(toRW(test))| val | x | y |
|---|---|---|
| 8 | 0.0000000 | 0.0000000 |
| 5 | 0.9182161 | 0.3960798 |
| 12 | 1.2602363 | -0.5436129 |
| 12 | 1.6022564 | -1.4833055 |
| 15 | 1.2602363 | -2.4229981 |
| 0 | 1.2602363 | -1.4229981 |
| 27 | 1.2602363 | -0.4229981 |
| 23 | 0.4581131 | 0.1741605 |
| 15 | 0.1160929 | -0.7655321 |
| 18 | -0.7499325 | -1.2655321 |
| 12 | -0.4079123 | -2.2052247 |
| 4 | 0.3942108 | -1.6080662 |
Now make a plot function to draw the “random” walk.
library(ggplot2)
plotRW <- function(rwData){
rwPlot <- ggplot(rwData, aes(x=x, y=y, group="1")) +
geom_path(aes(color = factor(val)), size=0.5) +
coord_fixed(ratio = 1) +
theme_bw() +
theme(line = element_blank(),
text = element_blank(),
line = element_blank(),
legend.position="none",
panel.border = element_blank(),
panel.background = element_blank())
return(rwPlot)
}Now to test it out.
plotRW(toRW(stringToVec("Nicholas Strayer")))